Nonlinear Control Systems
Partial differential equations for nonlinear control systems are important for a variety of technical applications. Examples are smart or morphing structures, temperature control in the steel production, and reactors of (bio-) chemical engineering. The goal is, for instance, to adjust a particular form of a mechanical structure or a particular temperature profile. This can be performed by so-called trajectory control concepts. In contrast to many other concepts, we use here partial differential equation models and therefore the full physical information.
In particular, nonlinear partial differential equations of parabolic type are analyzed and numerically solved. Some mathematical tools, which are employed, are semigroup theory and entropy methods. The Ph.D. projects will be conducted with the participation of the following professors from engineering and mathematics: Arnold, Jüngel, Kugi.
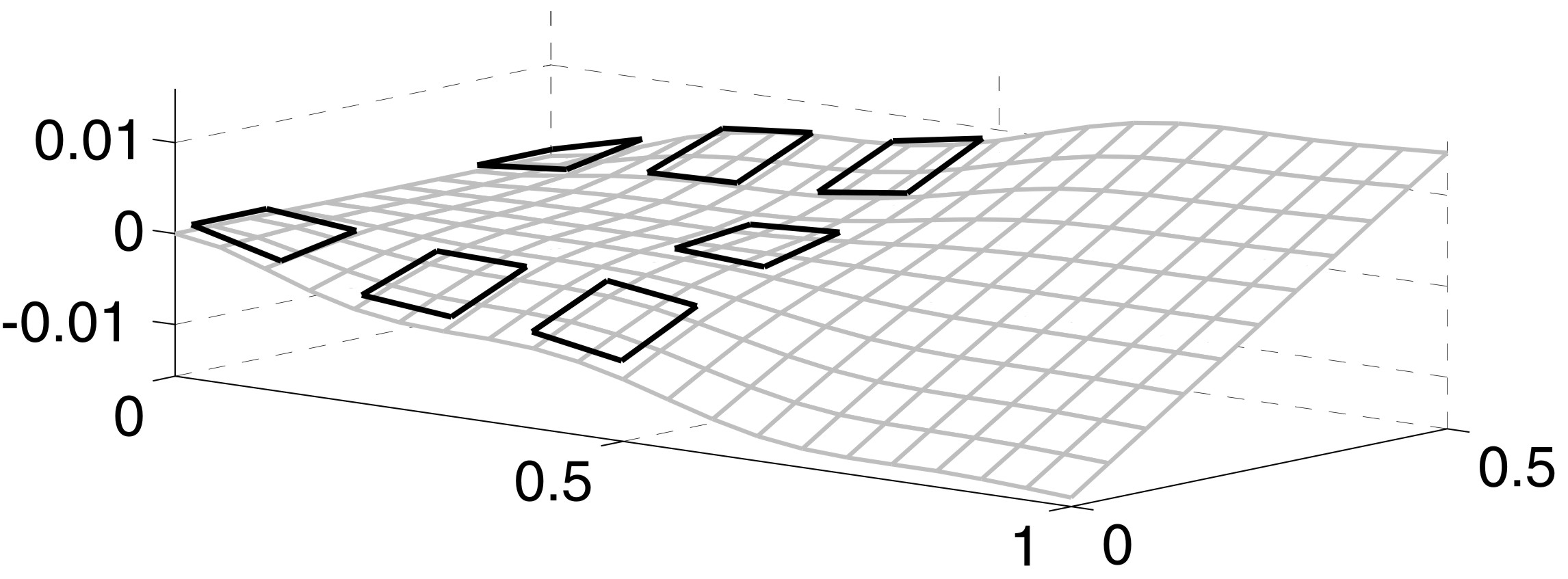
Control of an airfoil shape by piezo-electric actors